Los Números Complejos

Un Número Complejo es una expresión del tipo
z = a + bi
donde a y b son números reales e i es un símbolo.Representación Algebráica o Binómica de un número complejo
El siguiente es un número complejo z = x+iy
Re(z)= x, parte real
Im(z)=y, parte imaginaria
Representación Cartesiana
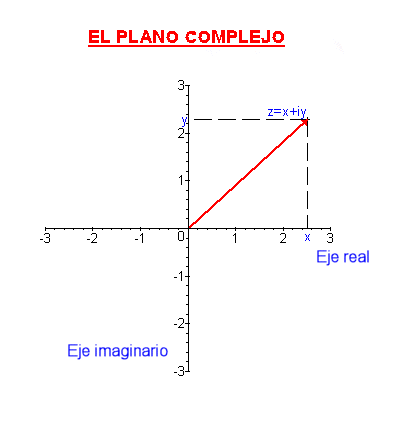
Im(z)=y, parte imaginaria
Representación Cartesiana

Propiedad de Igualdad entre Números Complejos
La igualdad de números complejos se define así:
 Esto es, dos complejos son iguales si y sólo si sus partes reales son iguales y sus partes imaginarias son iguales
Esto es, dos complejos son iguales si y sólo si sus partes reales son iguales y sus partes imaginarias son iguales
Operaciones de Números Complejos
SUMA
Sean z1 = a1 + b1i y z2 = a2 + b2i dos números complejos. Entonces la suma de z1 con z2, denotada por z1 + z2 es el número complejo
z1 + z2 = (a1 + a2) + (b1 + b2)i
Es decir, para sumar números complejos simplemente se suman sus componentes correspondientes.
Ejemplo. Para sumar z1 = 3 + 2i con z2 = −8 + 4i hacemos,
z1 + z2 = (3 + 2i) + (−8 + 4i) = (3−8) + (2 + 4)i z1 + z2 = −5 + 6i
Existencia del elemento neutro aditivo
El elemento neutro es 0 + 0 i , puesto que
(a + b.i) + (0 + 0 i) = (a + 0) + i (b + 0) = a + b.i
Propiedades
Conmutativa Dados dos números complejos a + b.i y c + d.i se tiene la igualdad:
(a + b.i) + (c + d.i) = (c + d.i) + (a + b.i)
Asociativa Dados tres complejos a + b.i, c + d.i y e + f.i , se cumple:
[(a + b.i) + (c + d.i)] + (e + f.i) = (a + b.i) + [(c + d.i) + (e + f.i)]
Existencia del inverso aditivo
El inverso aditivo de un número complejo cualquiera a + b.i es (- a - b.i):
(a + b.i) + (-a - b.i) = 0 + 0 i= 0
RESTA
Sean Z = a + bi y W = c+di dos números complejos, entonces la diferencia o resta entre Z y W viene dada por
Z −W = (a−c) + (b−d)i
Ejemplo. Sean Z = 4 + 7i y W = 2 + 3i. Entonces
Z −W = (4−2) + (7−3)i = 2 + 4i
PRODUCTO
Sean Z = a + bi y W = c + di definimos su producto, mediante la fórmula
Z ·W = (ac−bd) + (ad + bc)i
Ejemplo. Z = 8 y W = 3+2i. Entonces para hallar Z ·W
Z ·W = 8(3 + 2i) = 24 + 16i
Propiedades
Conmutativa
Dados dos complejos a + b.i y c + d.i , se cumple que:(a + b.i).(c + d.i) = (c + d.i) (a + b.i)
Asociativa
Dados los complejos a + bi, c + d.i y e + f.i se cumple que:[(a + b.i) (c + d.i)](e + f.i) = (a + b.i) [(c + d.i) (e + f.i)]
Distributiva
Dados tres números complejos a + b.i, c + d.i y e + f.i, se cumple:
(a + b.i).[(c + d.i) + (e + f.i)] = (a + b.i) (c + d.i) + (a + b.i).(e + f.i)
Existencia del elemento neutro multiplicativo
El elemento neutro del producto es 1 + 0 · i = 1, puesto que para cualquier complejo
a + b.i , (a + b.i) (1 + 0. i) = (a + b.i).1 = a + b.i.
El elemento neutro es el uno.
El conjugado de Z
Si Z = a + bi es un número complejo, entonces el Conjugado de Z, denotado por Z, es otro número complejo definido por
El Módulo de Z
Si Z = a+bi es un número complejo, el Módulo de Z es el número real
Existencia del elemento inverso multiplicativo
Dado un complejo cualquiera a + b.i , distinto de 0 + 0 i , existe otro complejo que, multiplicado por él,da el elemento neutro del producto, es decir, 1 + 0 i.
Demostración:
(a + b.i) (x + y.i) = 1 + 0 i
(a + b.i).(x + y.i) = (ax - by) + (ay + bx) i . Por tanto ha de ser:
ax - by = 1, multiplicando por a se tiene: a² x - aby = a
bx + ay = 0, multiplicando por b se tiene: b² x + aby = 0
Sumando (a² + b²).x = a ⇒ x = a/(a² + b²)
Despejando y en la segunda ecuación:
El inverso de un número complejo z = a + b.i , se suele denotar por 1/z ó z-1.
Por tanto, si z = a + b.i ,
1/z = a/(a² + b²) - b.i/(a² + b²)
División
La división es la operación inversa de la multiplicación. Esto es, dividir un número complejo entre otro es el resultado de multiplicar el primero por el inverso del segundo.
Propiedades del conjugado y del módulo de un complejo
Lunes, 5 de Octubre del 2015
Forma polar de un complejo
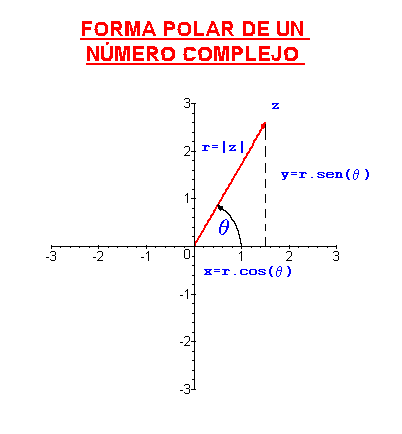
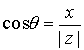 ,
, 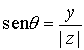 .
.
Producto
La forma polar de un número complejo es especialmente cómoda a la hora de multiplicar, ya que basta con multiplicar los módulos y sumar los argumentos, es decir, si 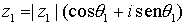 , y
, y 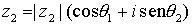 , entonces:
, entonces:
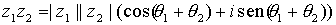
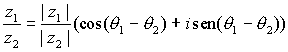 ,
siempre que
,
siempre que 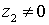 .
.
Del mismo modo se puede calcular el cociente de un complejo por otro no nulo sin más que dividir los módulos y restar los argumentos:
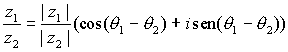 ,
,
Potencias y Raíces
Supongamos que Z = |Z|(cosθ+i senθ), y n es un entero positivo, entonces se obtiene:
Zn = |Z|n(cos(n·θ) + i sen(n·θ))
Esta relación, que se conoce con el nombre de Fórmula de Moivre, nos da un algoritmo bastante eficiente para hallar la potencia nésima de cualquier número complejo en forma polar.
Ejemplo. Sea Z = 2(cos30o + i sen30o). Calcule la potencia de orden cinco de este número, es decir, Z5.
Z5 = 25(cos(5·30o) + i sen(5·30o)) Z5 = 32(cos150o + i sen150o)
Sea Z = |Z|(cosθ + isenθ), entonces
Ejemplo. Hallar todas las raíces cúbicas de Z = 8(cos30o + isen30o)
con K = 0, 1, 2. Sustituyendo estos valores de k en la expresión de arriba nos da las tres raíces cúbicas
Círculo
Si Zo es un número complejo y r es un número positivo
|Z - Zo| = r
Z=x+iy
Zo= xo+iyo
|(x+iy) - (xo+iyo)| = r
(x-xo)2 + (y-yo)2 = r2 Ec. circunferencia de C(xo,yo) y radio r
Si Zo es un número complejo y r es un número positivo
|Z - Zo| = r
Z=x+iy
Zo= xo+iyo
|(x+iy) - (xo+iyo)| = r
(x-xo)2 + (y-yo)2 = r2 Ec. circunferencia de C(xo,yo) y radio r
|z- a| >r
EJEMPLO
Recta
Y = mx+b ------ Ec. de la recta bisectriz
Lunes, 12 de Octubre del 2015
Funciones de Variable Compleja
f: C-C
z-w=f(z)
w= Re[f(z)] + i Im [f(z)]
Si z= x+iy --- f(z)= f(x,y)
Re[f(z)] = u(x,y)
Im [f(z)]= v(x,y)
EJEMPLOS
Representaciones Gráficas
No es posible representar f(z), ya que se requiere R4 , pero es posible otras opciones como las siguientes:
- Representar la Re[f(z)]
- Representar la Im[f(z)]
- El módulo de f(z): |f(z)|
- El argumento principal
- Representar en el plano complejo la posición de sus ceros y sus polos.
- Representar las curvas de nivel de la parte real e imaginaria.
EJEMPLO
Sea f(z) = 6z-5+9i
f(x,y) = (6x-5) + i(6y+9)
Representa:
a.Re[f(z)] = u (x,y) = 6x-5 ---- superficie (plano)
b.Im[f(z)] = v (x,y) = 6y+9
a. Si z=u(x,y)---z=6x-5 Ec. plano con generatriz paralela al eje OY
Transformaciones del plano complejo
Una representación alternativa consiste en graficar las imágenes de rectas en el plano complejo.
EJEMPLO
w= f(z) =z2 = (x2- y2) + i2xy
Límites
Una función f(z) se dice que tiene límite w0 cuando z tiende a z0, y
se
escribe:
En términos matemáticos
0<|z-z0|<ẟ garantiza que |f(z)-L|<Ԑ
Propiedades
Lunes, 19 de Octubre del 2015
Continuidad
Una función, f(z), se dice que es continua en un punto, z0, si existen los valores de f(z0) y de lim f(z) z--z0
y ambos coinciden. Es decir:
EJERCICIO
Se pueden presentar dos tipos de discontinuidad:
- Inevitable: si no existe límite de f(z) cuando z---zo
- Evitable; si existe límite de f(z) cuando z---zo, pero no existe f(zo).Por tanto se debe REDEFINIR, para transformar a la función en continua en zo.
Análisis de continuidad
Derivación
Supóngase que f(z) es una función de variable compleja definida en una vencindad de un punto zo. La derivada de f(z) en el punto z0 es:
Siempre y cuando el límite exista.
- Se puede utilizar también:
- Las reglas de derivación y propiedades de las derivadas de funciones de variable real se aplican en las funciones de variable compleja.
EJEMPLO
Lunes, 26 de Octubre de 2015
Ecuaciones de Cauchy-Riemann (ECR)
Sea f(z) = u (x,y) + iv(x,y), una función de variable compleja, se dice que es analítica si se cumplen las ECR:
Teorema: Sea f(z)=u(x, y)+iv(x, y) una función definida en alguna región D que contiene a Zo y que tiene primeras derivadas parciales continuas y que satisfacen las ECR en Zo entonces f'(Zo) existe.
Coordenas Conjugadas
Un par de funciones u(x, y) y v(x, y) de variables reales x, y que satisfacen las
ecuaciones de Cauchy-Riemann se dice que son conjugadas.
Funciones Analíticas
-Se dice que f es analítica en Ω cuando es derivable en todos los puntos de Ω.
-Si f(z) es analítica en todo el plano complejo se dice que f es función entera.
-Las funciones analíticas se denominan también holomorfas o regulares.
- La derivada de una función analítica, también es analítica.
La función f(z) = *z*2 es derivable en z=0 pero no es analítica en dicho punto. Ya
que:
y éste último límite existe si, y sólo si z=0. Por tanto, no existe ningún entorno de 0 donde
la función sea derivable.
EJEMPLO
Funciones Armónicas
Sea f(z)= u(x,y) + iv (x,y) una función analítica, u ^ v se dice que son funciones armónicas y satisfacen:
Se dice que "u" es la conjugada armónica de "v" y "v" es la conjugada armónica de "u".
29 de Octubre del 2015
Funciones Trascendentes básicas
Bibliografía
http://www.fisicanet.com.ar/matematica/numeros_complejos/ap03_numeros_complejos.php
http://wmatem.eis.uva.es/~matpag/CONTENIDOS/Complejos/marco_complejos.htm
https://algebraunq.wikispaces.com/file/view/Distancia+entre+dos+n%C3%BAmeros+complejos.pdf
http://www2.caminos.upm.es/Departamentos/matematicas/Fdistancia/PIE/Analisis%20matematico/Temas/C02_Funciones_complejas.pdf
http://ocw.uc3m.es/matematicas/ampliacion-de-matematicas-i/soluciones/solu2.pdf
http://www.dmae.upct.es/~jose/ampcal/complex.pdf




































No hay comentarios:
Publicar un comentario