Diciembre

Serie de Taylor

Por sustitución

Ejemplo:

Por derivación

Ejemplo:   

Por integración

Ejemplo:

SERIE DE LAURENT

Si la función no es analítica en z=0, no admite desarrollo mediante una serie de Taylor, pero admite un desarrollo mediante una serie de Laurent.

Propiedad 1

Si f es analítica en el anillo  r1< |z-z0| < r2, entonces para z en este anillo 

Se llama serie de Laurent, o serie doble, a una serie definida de la forma

donde; Cn, C-n son coeficientes de la serie

 parte analítica

parte principal

Ejemplo:

TEOREMA DE LOS RESIDUOS

Singularidades

Un punto z0 es un punto singular de f(z), si f(z) es analítica en algún punto de toda la vecindad de z0, excepto en z0 mismo.

Las singularidades pueden ser de varios tipos:

-Aisladas

-Polo

-Punto de ramificación

-Removible

-Esencial

-En el infinito

Ejemplo:

Residuos

Si la función f(z) tiene polos en Zj, y f(z) es:

en este caso f(z) tiene un polo de orden "m" en z0=zj y el coeficiente de "b1" recibe el nombre de residuo de f(z) y se denota por:

Aplicaciones del Teorema del Residuo

PRIMER TIPO

Se puede evaluar integrales convergentes del tipo:

siempre y cuando:

1) p(x) ^ q(x) son polinomios de coeficientes reales

2) q(x) diferente de 0

3) El grado de q(x) es por lo menos de dos grados mayor que p(x)

Ejemplo:

SEGUNDO TIPO

Ejemplo:

Funciones Periódicas y Ortogonales

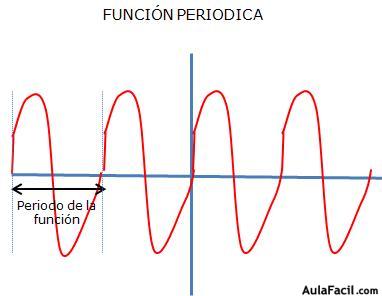
Una función f(x) es periódica, de período T, si para todo número entero z, se verifica:

f(x) = f(x + zT)

Ejemplo: Periodo de la siguiente función

Función Ortogonal

Dos funciones f1 y f2 son ortogonales en el intervalo [a, b] si

Por ejemplo, las funciones f1(x) = x 2 y f2(x) = x 3 son ortogonales en el intervalo [−1, 1] puesto que 

Se dice que un conjunto de funciones {ϕn} ∞ n=0 es ortogonal en el intervalo [a, b] si

Si {ϕn} ∞ n=0 es un conjunto ortogonal de funciones en el intervalo [a, b] con la propiedad de que ∥ϕn∥ = 1 para cualquier n, entonces se dice que {ϕn} ∞ n=0 es un conjunto ortonormal en el intervalo [a, b].

Propiedades

Supongamos que u y v son vectores en el espacio tridimensional. El producto interno (u, v) de los vectores, que también se escribe u.v, posee las propiedades siguientes:

i) (u, v) = (v, u)

ii) (ku, v) = k(u, v), donde k es un escalar

iii) (u, u)= 0, si u= 0,y  (u,u) > 0 si u ≠ 0

iv) (u + v, w) = (u, w) + (v, w).

Ejemplo:

Series de Fourier

La serie de Fourier en una función f definida en el intervalo (-p,p) es

Desarrollos de series de Fourier de funciones pares e impares

- Una función es par si verifica f(−x) = f(x) para cualquier x, 

- La función es impar si f(−x) = −f(x). 

En un intervalo simétrico como (−p, p) la gráfica de una función par posee simetría respecto al eje y, mientras que la gráfica de una función impar posee simetría con respecto al origen.

Estas funciones verifican las siguientes propiedades:

• El producto de dos funciones pares es par. 

• El producto de dos funciones impares es par. 

• El producto de una funci´on par y una impar es impar. 

• La suma o la diferencia de dos funciones pares es par. 

• La suma o la diferencia de dos funciones impares es impar. 

• Si f es par, entonces ∫ a −a f(x) dx = 2 ∫ a 0 f(x) dx. 

• Si f es impar, entonces ∫ a −a f(x) dx = 0.

Ejemplo:

Aproximación mediante una serie finita de Fourier

En la expresión de la descomposición en Serie de Fourier de una función periódica aparece un sumatorio que incluye un número ilimitado de elementos.  SK(t), que es aquella descomposición armónica en la que se tienen en cuenta sólo los primeros K elementos de la Serie de Fourier, o sea:

Si se aproxima la función f(t) mediante la serie finita de Fourier SK(t), se obtiene la expresión:

donde εK(t) es el error debido a la aproximación mediante la Serie de Fourier de K términos. Para determinar la calidad de la aproximación es más adecuada una medida cuantitativa del error global por período, para ello se utiliza el error cuadrático medio:

 Ejemplo:

Bibliografía

http://www2.caminos.upm.es/Departamentos/matematicas/Fdistancia/PIE/Analisis%20matematico/Temas/C03_Series_Complejas.pdf

http://ocw.uc3m.es/matematicas/ampliacion-de-matematicas-i/lecturas/cap6.pdf
http://www.vitutor.com/fun/2/a_11.html
http://www.dma.uvigo.es/~aurea/Transparencias_tema2.pdf
https://wilfridomtz.files.wordpress.com/2014/09/capitulo-10.pdf
http://grupo_ene.webs.uvigo.es/publicaciones/Apuntes_Fourier.pdf